湖南行測數量關系“隔板模型”排列組合
在行測數量關系考試中,排列組合是很多人又愛又恨的一個考點,對文科生來講尤其如此,愛它是因為計算量相對不大,恨它是因為計數時經常出現重復或遺漏的情況。其實排列組合中的一些問題是有固定解題思路的,也有一些常見的解題模型。本文,湖南公務員考試網小編就給大家分享排列組合中一種特殊模型——“隔板模型”。
“隔板模型”的特征是:n個相同元素分給m個不同對象,每個對象至少分一個元素,求所有可能的分法。“隔板模型”的解題思路是:將n個元素排成一排,在n個元素之間形成的n-1個間隙中放置m-1塊隔板,即可把它隔成m份,這樣所有不同的插入方法就是n個相同的元素分給m個不同對象的所有情況數,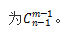
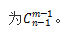
例1、共有10本完全相同的書分到4個班里,每個班至少要分到一本書,共有幾種不同分法?
A.84
B.75
C.64
D.45
【解析】答案選A。先將10本相同的書排成一排,10本書之間出現了10-1=9個空隙,現在我們用4-1=3個擋板插入這9個空隙中,就把10本書隔成4份,正好分給4個班級;從9個空選3個插入3個相同擋板,不考慮順序,按照公式計算出有84種。故正確答案為A。
例2、共有6本完全相同的書分到4個班里,共有多少種不同分法?
A.84
B.75
C.64
D.45
【解析】答案選A。由于會有不放書的班級,因此需要將問題轉化為標準的隔板模型。先從每個班級借一本書,則現在有10本書,問題就轉化為“將10本完全相同的書分給4個班,每班至少分到一本”。從10本書排成一排所形成的10-1=9個空隙里選擇3個空隙插入隔板,就把10本書隔成4份,正好分給4個班級,每個班至少一本書,按照公式計算出有84種。則不同的分法故正確答案為A。
例3、共有14本完全相同的書分到4個班里,每個班至少分到兩本書,共有多少種不同分法?
A.84
B.75
C.64
D.45
【解析】答案選A。由于每個班級至少分兩本,因此需要將問題轉化為標準的隔板模型。每個班級先發(fā)1本書,還剩10本,則問題轉化為“將10本完全相同的書分給4個班,每班至少分到一本”。從10本書排成一排所形成的10-1=9個空隙里選擇3個空隙插入隔板,就把10本書隔成4份,正好分給4個班級,按照公式計算出有84種。故正確答案為A。
通過上面三個例子對比,大家會發(fā)現雖然下面兩個例子與“隔板法”題型特征不符,但是我們可以通過轉換使其滿足條件,最終還是可以借助公式來解題。希望同學們在平日的學習中能夠多多練習,真正把所學方法內化于心,外化于行,做到信手拈來!



點擊分享此信息:
 相關文章
相關文章


